Das Inverter IC CD4069 wird als RC Oszillator verwendet und am Ausgang werden 2 LEDs als Wechselblinker geschaltet.
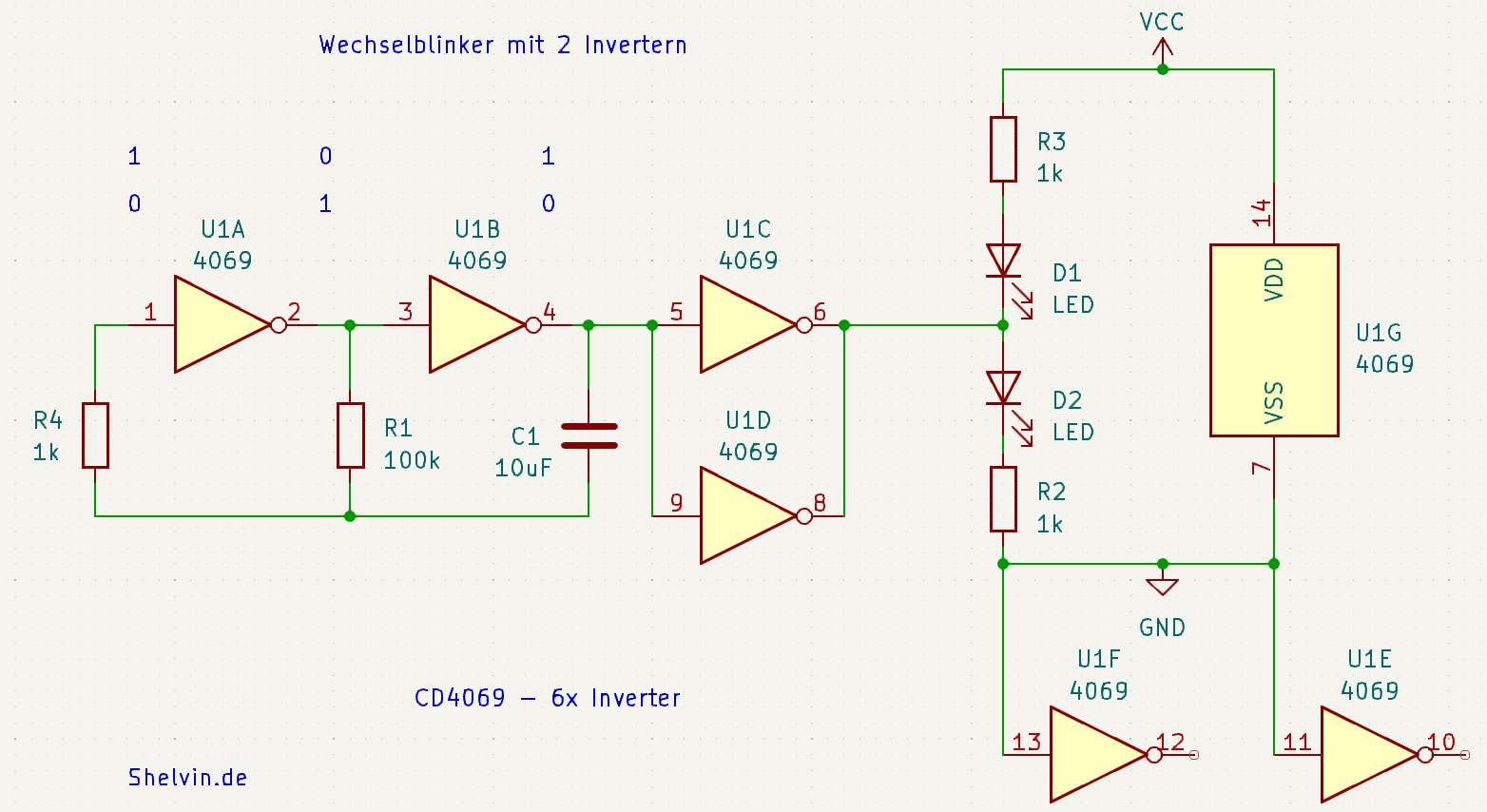
und nun das ganze auf dem Breadboard aufgebaut Weiterlesen

Das Inverter IC CD4069 wird als RC Oszillator verwendet und am Ausgang werden 2 LEDs als Wechselblinker geschaltet.

und nun das ganze auf dem Breadboard aufgebaut Weiterlesen
So kann eine einfache Konstantstromquelle aufgebaut werden mit einen Spannungsregler LM317 und einem Widerstand. Der Widerstand bestimmt die Stromstärke.
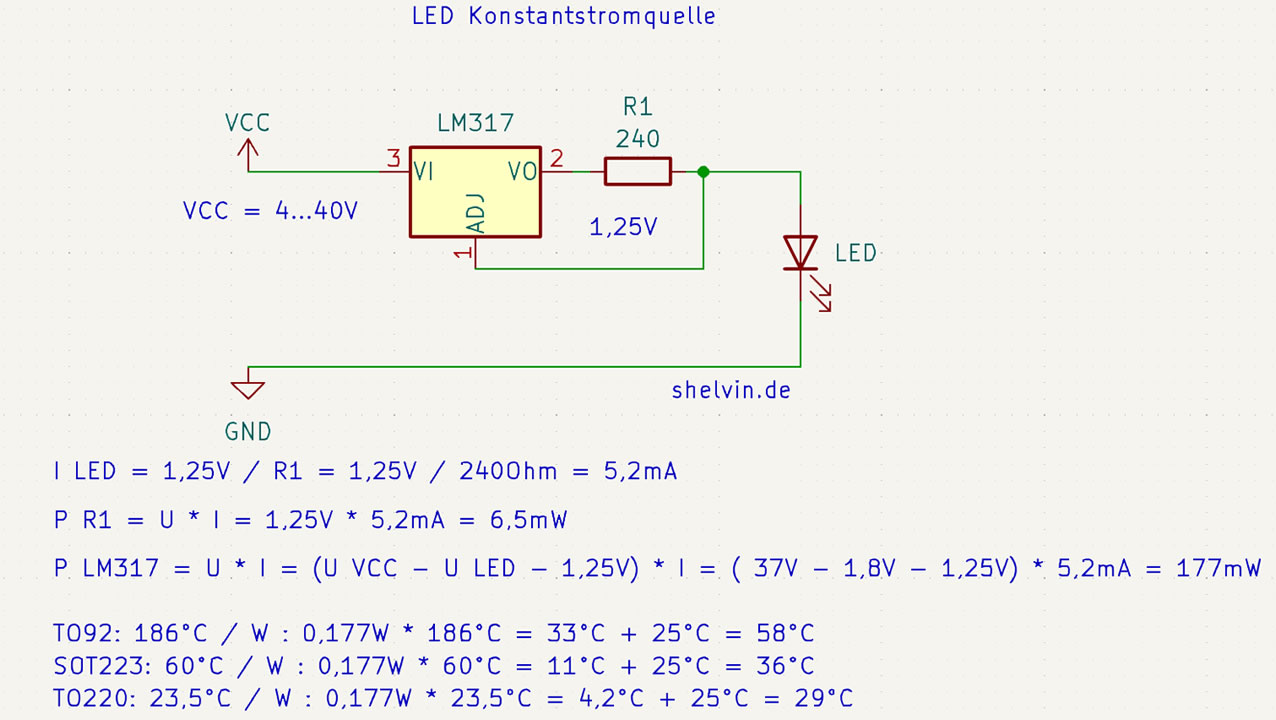
Der Aufbau Weiterlesen
Der Spannungsregler LM317 kann als Zener Diode eingesetzt werden für 1,5V mit 1,5A.
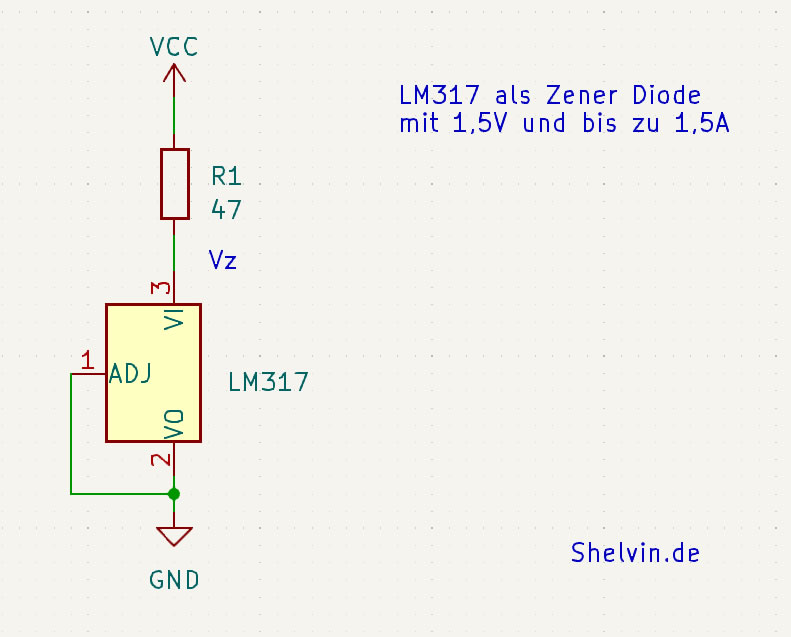
Interner Aufbau LM317 Weiterlesen
Schaltungen für einstellbare Linear-Spannungsregler zur Begrenzung der Ausgangsspannung wenn der Poti ausfällt. Für Positiv- und Negativ-Regler und für den Gleitkontakt am Adjust Anschluss oder an Masse.
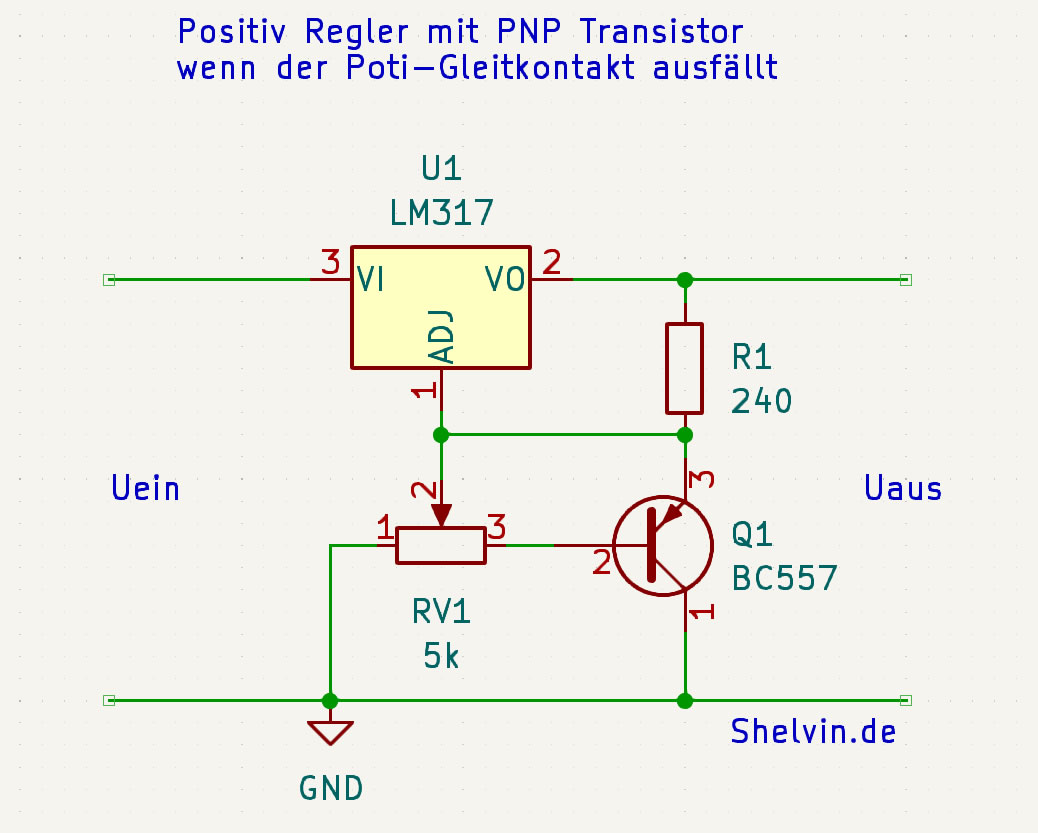
Ein einstellbarer Spannungsregler LM-317 mit Schutzschaltung, Dioden, Kapazitäten und dem Poti Transistor Trick.
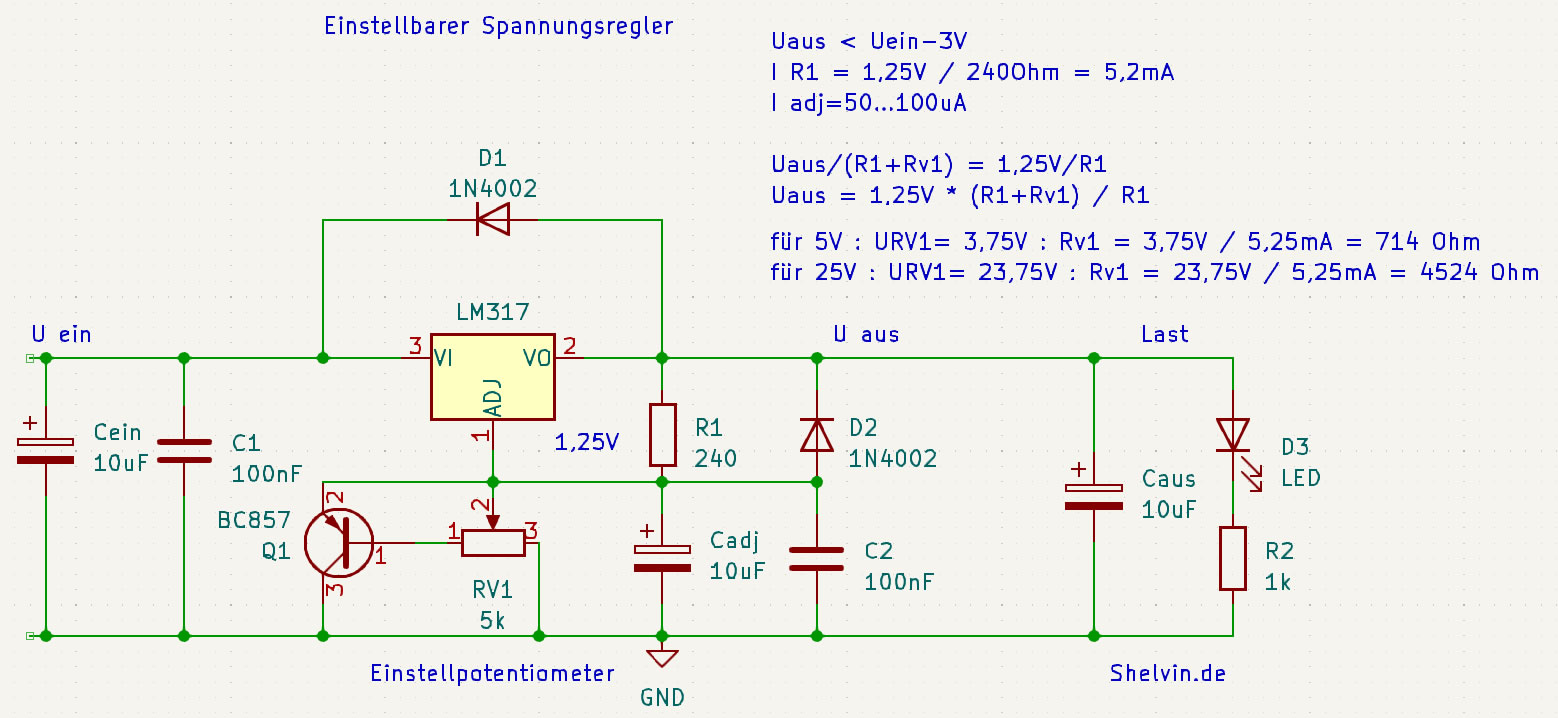
und hier die Erklärung zu Schaltung Weiterlesen
Eine Übersicht der häufig verwendeten Spannungsregler, Besonderheiten und die technischen Daten.
Die typische Schaltung mit einem Spannungsregler:
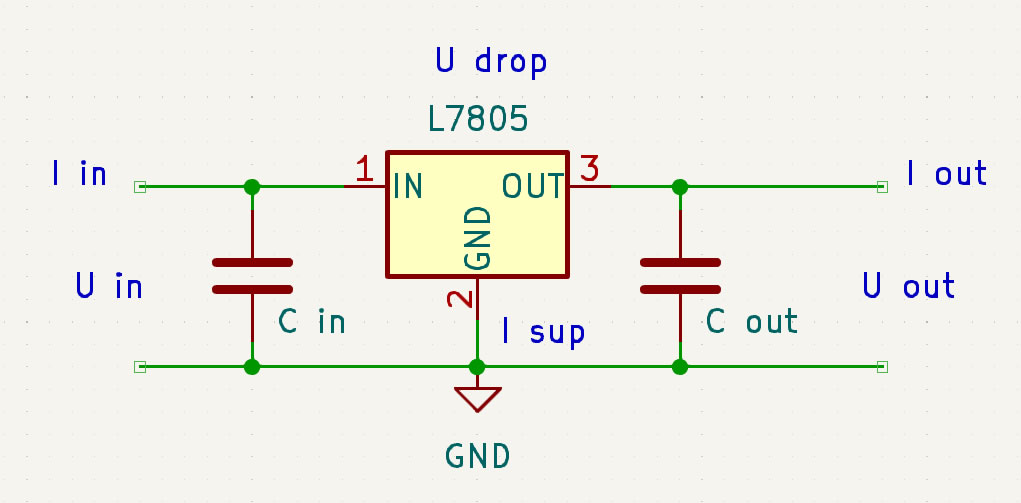
Die Spannungsregler Übersicht als Tabelle (pdf). Weiterlesen
Eine einfache LED Spannungsanzeige für das Breadboard umbauen. Hier wird auch erklärt worauf man achten sollte, wie die Anzeige aufgebaute ist und welche Fehler ich gefunden habe.
Wenn nur ein einfaches Netzteil zur Verfügung steht und die Schaltung eine symetrische Spannung mit Masse benötigt, dann hilft diese einfache Schaltung mit einem Operationsverstärker. Sie erzeugt eine neue virtuelle Masse. Und dann noch ergänzt durch eine Stromverstärkung für hungrigere Schaltungen.
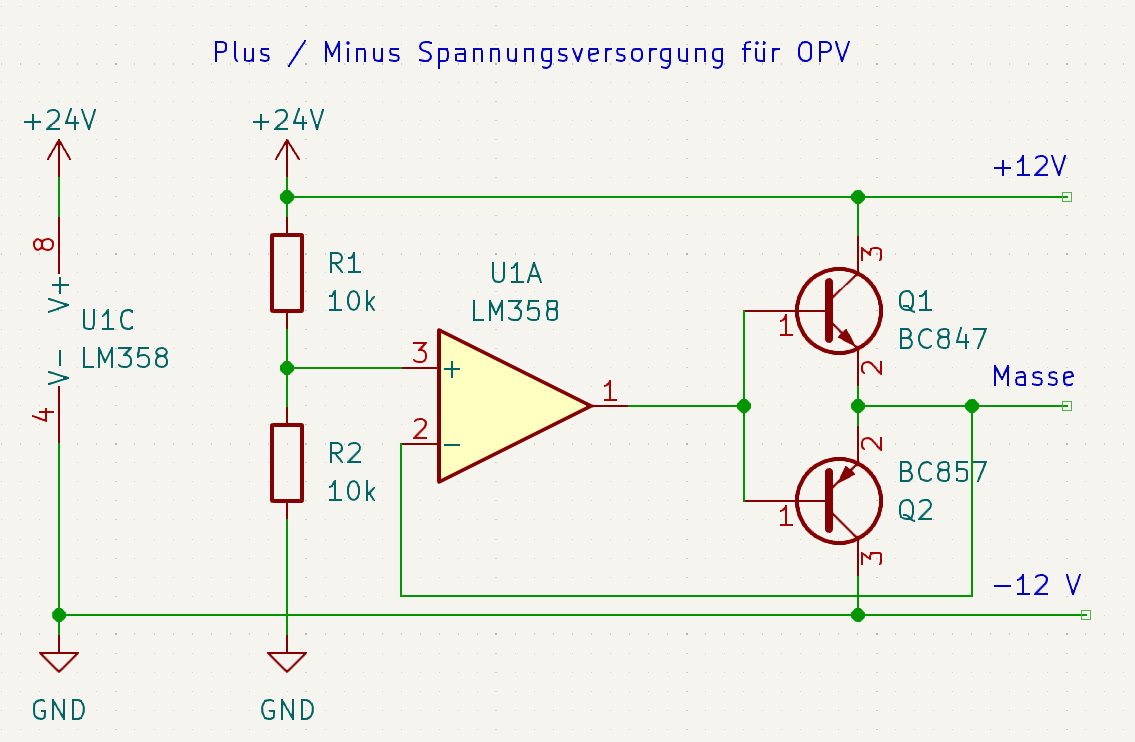
und hier die Erklärung dazu: Weiterlesen
Einige grundlegende Vertstärker Schaltungen mit dem Operationsverstärker
1. Der Spannungsfolger
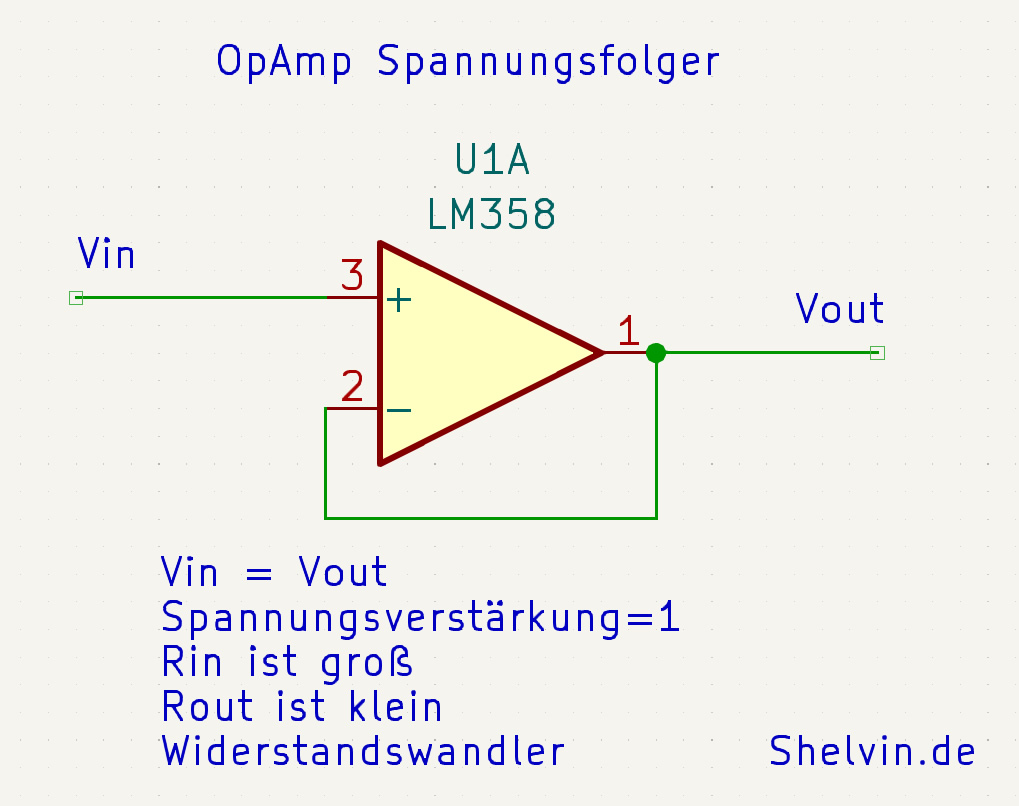
2. Der Verstärker Weiterlesen
Wie funktioniert ein Operationsverstärker? Eine kleine Einführung und die Schaltung als Spannungsfolger.
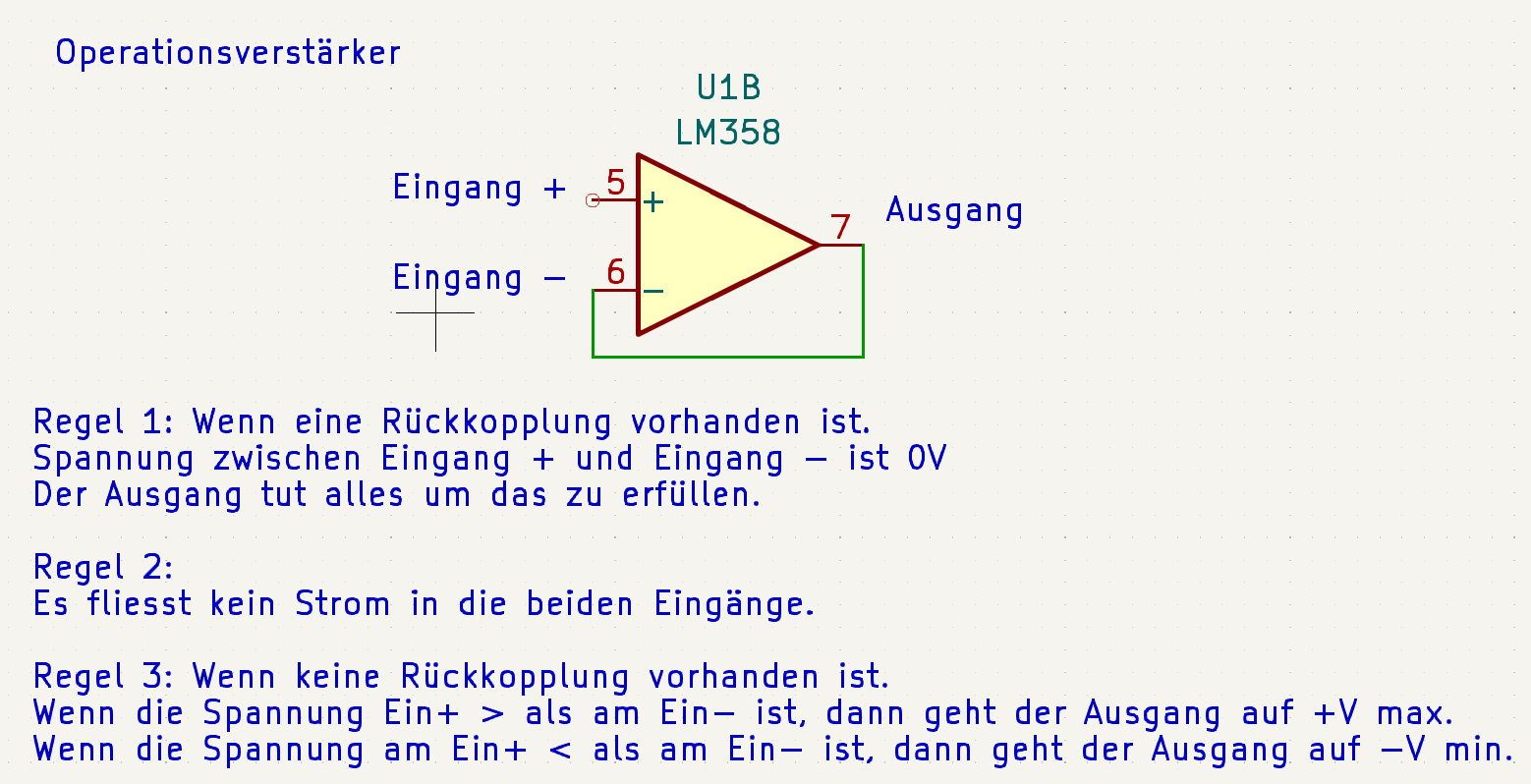
Aufbau als Spannungsfolger Weiterlesen