Aus den letzten beiden Artikeln Arduino FFT berechnen und 5110 Grafik ausgeben ist nun eine Arduino Uno FFT Berechnung mit Grafik Ausgabe geworden.
Für die Grafik Ausgaben wurde die Library von Henning Karlsen installiert und verwendet.
Das Programm berechnet verschiedene Wellenformen
– Ein Rechtecksignal
– Ein Sinus Signal
– Zwei addierte Sinus Wellen
– Eine Frequenzmodulation
und gibt das Frequenzspektrum von 0 – 2520 Hz aus, in 40 Hz Schritten.
Die Frequenz wird nach jeder Berechnung um die Schrittweite 40 erhöht.
Die Rechteck Berechnung :
void rechteck(int amp, double fr) {
// Rechtecksignal erzeugen
phase = 0.0;
for(i=0; i < 128; i++) {
im[i] = 0; // Imaginärteil ist immer 0
if(phase < 0.5) {
re[i] = amp; // Realteil der Welle berechnen
}
else {
re[i] = -amp;
}
phase += fr/F_SAMPLE; // die Phase der Welle weitergehen
if(phase >= 1)phase -= 1;
}
}
Im loop() kann die gewünschte Wellenforn auskommentiert und verwendet werden.
void loop() {
rechteck(140, (double)freq); // Rechtecksignal berechnen
//sinus(90, (double)freq); // Sinus Signal berechnen
//sinusaddition(90, (double)freq, 50, 400); // 2 Sinussignale addieren
//fm(90, (double)freq, 800); // Frequenz Modulation
fix_fft(re,im,7,0); // die FFT der Messwerte berechnen
lcdOutFft(); // aus dem 5110 LCD ausgeben
freq += fstep; // Frequenz erhöhen
if(freq > fstep*N_WAVE) freq=fstep; // nach der maximalen Frequenz wieder auf den Startwert
}
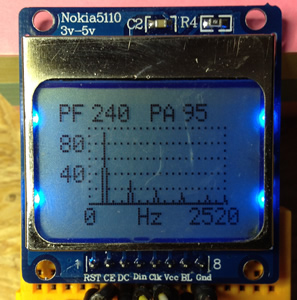
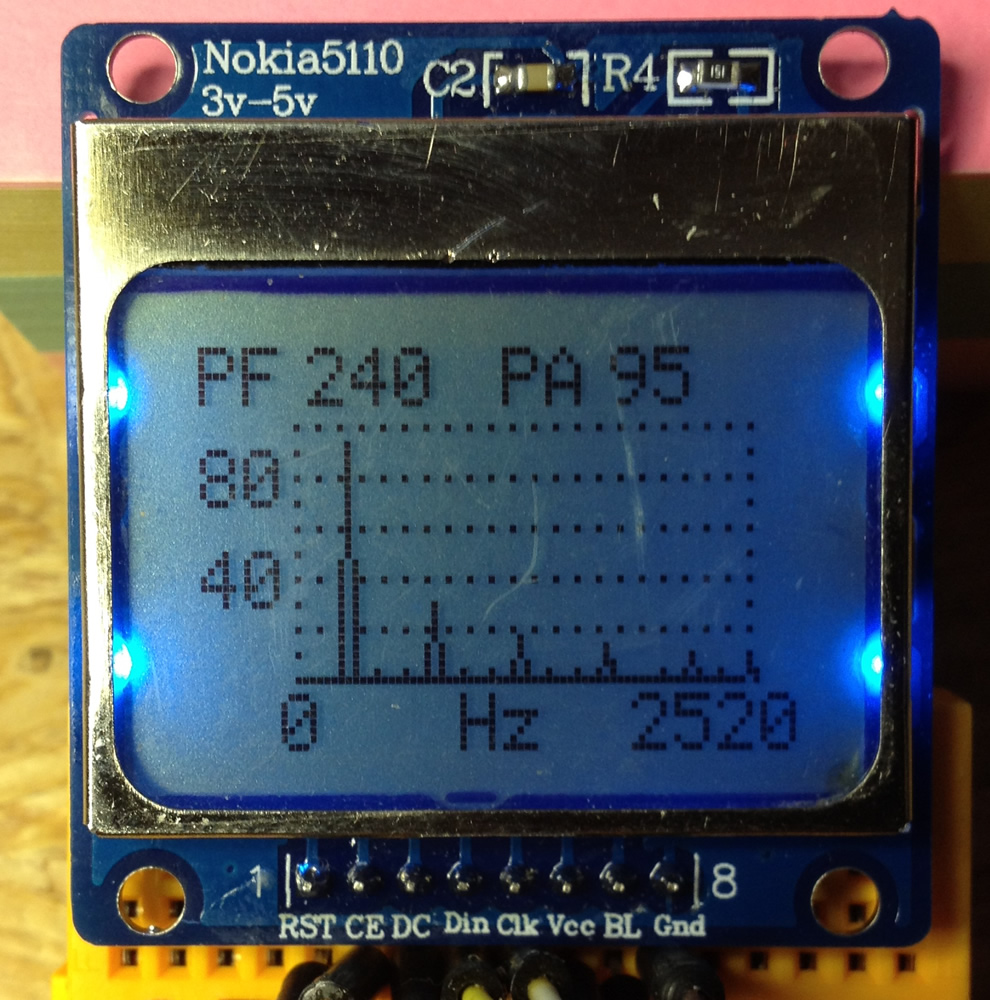
Das Ergebnis der FFT Berechnung wird auf dem LCD Display eines Nokia 5110 ausgegeben.
Die Skala links mit möglichen Werten von 0-10 hoch zu 0-100 wird auf Grund der größten Amplitude automatisch festgelegt. Oben werden dann noch die Frequenz PF mit der größten Amplitude PA ausgegeben. Punktierte Linien verbessern die Lesbarkeit.
Der Arduino Uno ist an seiner Grenze angekommen, sodass ich das Sinewave Feld wieder auf char (8-Bit) zurück genommen habe.
Und hier nun das komplette Programm
// FFT Berechnung und Ausgabe auf einen 5110 LCD Display
//
// Änderungen Version 0.6
// 5110 LCD Ausgabe hinzugefügt. Library von http://www.rinkydinkelectronics.com/library.php?id=48
// Sinewave[] auf char (8-Bit) zurück gesetzt, sonst wird der Speicher beim Arduino Uno knapp.
//
// Matthias Busse 25.4.2015 Version 0.6
#define N_WAVE 256 // volle Länge der Sinewave[] möglich 16, 64, 256, 1024 ...
#define LOG2_N_WAVE 8 // log2(N_WAVE)
#define F_SAMPLE 5120 // 5120/128 = 40Hz per FFT "bin"
#define AMP_CARRIER 68 // amplitude of each "carrier" wave
#include <LCD5110_Graph.h>
LCD5110 lcd(8,9,10,11,12); // Clk, Din, DC, RST, CE und noch GND>GND, 5V>VCC, 3,3V>BL
extern uint8_t SmallFont[];
int i, k, l, glinks=14, grechts=glinks+63, goben=9, gunten=39;
double freq, phase;
int pf, pa; // Peak Frequenz und Peak Amplitude
int fstep=40; // Frequenz Schrittweite
int im[N_WAVE/2];
int re[N_WAVE/2];
char Sinewave[N_WAVE/2] = { // 128 Werte, die halbe positive Sinuswelle
0, 3, 6, 9, 12, 15, 18, 21,
24, 28, 31, 34, 37, 40, 43, 46,
48, 51, 54, 57, 60, 63, 65, 68,
71, 73, 76, 78, 81, 83, 85, 88,
90, 92, 94, 96, 98, 100, 102, 104,
106, 108, 109, 111, 112, 114, 115, 117,
118, 119, 120, 121, 122, 123, 124, 124,
125, 126, 126, 127, 127, 127, 127, 127,
127, 127, 127, 127, 127, 127, 126, 126,
125, 124, 124, 123, 122, 121, 120, 119,
118, 117, 115, 114, 112, 111, 109, 108,
106, 104, 102, 100, 98, 96, 94, 92,
90, 88, 85, 83, 81, 78, 76, 73,
71, 68, 65, 63, 60, 57, 54, 51,
48, 46, 43, 40, 37, 34, 31, 28,
24, 21, 18, 15, 12, 9, 6, 3,
};
void setup() {
Serial.begin(57600);
lcd.InitLCD(60);
lcd.setFont(SmallFont);
lcd.clrScr();
lcd.print("Spektrum", CENTER, 0);
lcd.print("Version 0.6", CENTER, 15);
lcd.print("Matthias Busse", CENTER, 30);
lcd.update();
delay(1000);
lcd.clrScr();
freq = fstep;
}
void loop() {
rechteck(140, (double)freq); // Rechtecksignal berechnen
//sinus(90, (double)freq); // Sinus Signal berechnen
//sinusaddition(90, (double)freq, 50, 400); // 2 Sinussignale addieren
//fm(90, (double)freq, 800); // Frequenz Modulation
fix_fft(re,im,7,0); // die FFT der Messwerte berechnen
lcdOutFft(); // aus dem 5110 LCD ausgeben
freq += fstep; // Frequenz erhöhen
if(freq > fstep*N_WAVE) freq=fstep; // nach der maximalen Frequenz wieder auf den Startwert
}
int fix_fft(int fr[], int fi[], int m, int inverse){
// fix_fft() - Forwärts oder Inverse Fast Fourier Transform.
// fr[n],fi[n] Real und Imaginär Teil Felder für Eingabe und Ergebnis
// mit 0 <= n < 2**m;
// inverse=0 heisst forwärts transformieren (FFT), oder =1 für inverse iFFT.
int mr, nn, i, j, l, k, istep, n, scale, shift;
int qr, qi, tr, ti, wr, wi, idx;
n = 1 << m;
if (n > N_WAVE) return -1; /* max FFT size = N_WAVE */
mr = 0;
nn = n - 1;
scale = 0;
for (m=1; m <= nn; ++m) { /* decimation in time - re-order data */
l = n;
do { l >>= 1;
} while (mr+l > nn);
mr = (mr & (l-1)) + l;
if (mr <= m) continue;
tr = fr[m];
fr[m] = fr[mr];
fr[mr] = tr;
ti = fi[m];
fi[m] = fi[mr];
fi[mr] = ti;
}
l = 1;
k = LOG2_N_WAVE-1;
while (l < n) {
if (inverse) {
shift = 0; /* variable scaling, depending upon data */
for (i=0; i < n; ++i) {
j = fr[i];
if (j < 0) j = -j;
m = fi[i];
if (m < 0) m = -m;
if (j > 16383 || m > 16383) {
shift = 1;
break;
}
}
if (shift) ++scale;
}
else { // nicht invers
shift = 1;
}
istep = l << 1;
for (m=0; m < l; ++m) {
j = m << k;
if((idx = j+N_WAVE/4) >= 128) wr = -Sinewave[idx - 128];
else wr = Sinewave[idx];
if(j >= 128) wi = Sinewave[j];
else wi = -Sinewave[j];
if (inverse) wi = -wi;
if (shift) {
wr >>= 1;
wi >>= 1;
}
for (i=m; i < n; i+=istep) {
j = i + l;
tr = FIX_MPY(wr,fr[j]) - FIX_MPY(wi,fi[j]);
ti = FIX_MPY(wr,fi[j]) + FIX_MPY(wi,fr[j]);
qr = fr[i];
qi = fi[i];
if (shift) {
qr >>= 1;
qi >>= 1;
}
fr[j] = qr - tr;
fi[j] = qi - ti;
fr[i] = qr + tr;
fi[i] = qi + ti;
}
}
--k;
l = istep;
}
return scale;
}
inline int FIX_MPY(int a, int b) {
int c = ((int)a * (int)b) >> 6; /* shift right one less bit (i.e. 15-1) */
b = c & 0x01; /* last bit shifted out = rounding-bit */
a = (c >> 1) + b;/* last shift + rounding bit */
return a;
}
void rechteck(int amp, double fr) {
// Rechtecksignal erzeugen
phase = 0.0;
for(i=0; i < 128; i++) {
im[i] = 0; // Imaginärteil ist immer 0
if(phase < 0.5) {
re[i] = amp; // Realteil der Welle berechnen
}
else {
re[i] = -amp;
}
phase += fr/F_SAMPLE; // die Phase der Welle weitergehen
if(phase >= 1)phase -= 1;
}
}
void sinus(int amp, double fr) {
// Sinus Signal ausgeben
phase=0.0;
for(i=0; i < 128; i++) {
im[i] = 0; // Imaginärteil ist immer 0
re[i] = (int)(amp*sin(phase*2.0*PI)); // Welle berechnen
phase += fr/F_SAMPLE; // Phase von Welle weitergehen
if(phase >= 1) phase -= 1;
}
}
void sinusaddition(int amp1, double fr1, int amp2, double fr2) {
// Zwei Sinus Wellen addieren
double phase1=0.0, phase2=0.0;
for(i=0; i < 128; i++) {
im[i] = 0; // Imaginärteil ist immer 0
re[i] = (int)(amp1*sin(phase1*2.0*PI)); // Frequenz 1
re[i] += (int)(amp2*sin(phase2*2.0*PI)); // plus Frequenz 2
phase1 += fr1/F_SAMPLE; // Phase 1
if(phase1 >= 1)phase1 -= 1;
phase2 += fr2/F_SAMPLE; // Phase 2
if(phase2 >= 1)phase2 -= 1;
}
}
void fm(int amp1, double fr1, double fr2) {
// Fequenzmodulation
double dev=240, phase1=0.0, phase2=0.0;
for(i=0; i < 128; i++) {
im[i] = 0; // Imaginärteil ist immer 0
// FM modulate a "carrier" wave, having a frequency of f_tone2=1280Hz,
// with an "audio" wave having a frequency of f_tone1=240Hz
re[i] = (char)(amp1*sin(2*PI*phase2 + (dev/fr1)*sin(phase1*2*PI)));
phase1 += fr1/F_SAMPLE; // Phase 1
if(phase1 >= 1)phase1 -= 1;
phase2 += fr2/F_SAMPLE; // Phase 2
if(phase2 >= 1)phase2 -= 1;
}
}
void lcdOutFft() {
// FFT auf dem 5110 LCD ausgeben
// von Matthias Busse 25.4.2015 Version 1.0
int i, n, beschr, skalenteil, skalamax;
calc_pa_pf();
lcd.print("PF",0,0); // Peak Frequenz
lcd.printNumI(pf,15,0);
lcd.print("PA",42,0); // Peak Amplitude
lcd.printNumI(pa, 57,0);
lcd.drawLine(glinks,gunten,grechts,gunten); // Linie unten
lcd.print("0", glinks-3, 41); // Beschriftung unten
lcd.print("Hz", CENTER, 41);
lcd.print("2520", RIGHT, 41);
dotLineVert(glinks,goben,gunten); // Senkrechte Linie links
dotLineVert(grechts,goben,gunten);// Senkrechte Linie rechts
skalenteil = (gunten-goben)/5; // Pixel/5
if(pa < 100) { skalamax=100; beschr=40; } // Skala Maximalwert festlegen
if(pa < 50) { skalamax=50; beschr=20; }
if(pa < 25) { skalamax=25; beschr=10; }
if(pa < 10) { skalamax=10; beschr=4; }
i=gunten-(5*skalenteil);
dotLineHor(glinks,grechts,i); // Punktlinie horizontal
i=gunten-(4*skalenteil);
lcd.printNumI(beschr*2, 0, i-3); // Beschriftung links
dotLineHor(glinks,grechts,i); // Punktlinie horizontal
i=gunten-(3*skalenteil);
dotLineHor(glinks,grechts,i); // Punktlinie horizontal
i=gunten-(2*skalenteil);
lcd.printNumI(beschr, 0, i-3); // Beschriftung links
dotLineHor(glinks,grechts,i); // Punktlinie horizontal
i=gunten-(1*skalenteil);
dotLineHor(glinks,grechts,i); // Punktlinie horizontal
l=0;
n=0;
for(i=glinks; i <= grechts; i++) {
k=re[n]*5*skalenteil/skalamax;
lcd.drawLine(i,gunten-l,i+1,gunten-k);
l=k;
n++;
}
lcd.update();
delay(2000);
lcd.clrScr();
}
void dotLineHor(int x1, int x2, int y) {
// punktierte waagerechte Linie zeichnen
int m, n=0;
for(m=x1; m < x2; m++) {
if((n%3) == 0) lcd.setPixel(m,y);
n++;
}
}
void dotLineVert(int x, int y1, int y2) {
// punktierte senkrechte Linie zeichnen
int m, n=0;
for(m=y1; m < y2; m++) {
if((n%3) == 0) lcd.setPixel(x,m);
n++;
}
}
void calc_pa_pf() {
// höchste Amplitude (peak amp) und deren Frequenz (peak freq) berechnen
pf=0;
pa=0;
for (i=0; i < 64;i++){ // Die größe Amplitude gibt den maximalen Y-Achsenwert
re[i] = sqrt(re[i] * re[i] + im[i] * im[i]);
if(re[i] > pa) {
pa = re[i];
pf = i*fstep;
}
}
}
verwendet wurde
Hardware: Arduino Uno R3, Nokia 5110 Display 5V kompatibel
Software: Arduino 1.6.1, LCD Library, fix_fft Berechnung
von Matthias Busse


Hi Matthias,
ich kann kein Fenster, wie z.B. Hamming oder Blackman etc. entdecken. Ich das nicht wirklich wichtig für diesen Fall oder deinem Versuch? Ich probiere gerade eine FFT mit einem STM32duino aus und frage mich, ob ich die Kausalität beachten sollte/muss. Auch bei mir ist das Array aus Analogwerten nur ein Ausschnitt zur irgend einem Zeitpunkt und enthält damit an beiden Enden mitunter harmonische Anteile.
Gruß
Reiner